CRC는 Cyclic Redundancy Check의 약자로, 데이터의 정합성을 체크하는 방법 중 하나입니다. 주로 데이터를 송수신할 때 사용하며, 원본 데이터가 훼손이 없다는 것을 증명하기 위해 사용합니다.
CRC 관련 용어들
상세한 예제는 조금 아래에서 알아보기로 하고, 일반적으로 CRC 하면 사용하는 용어가 몇개 있습니다. 그걸 먼저 알아볼께요.
polynomial
CRC를 계산할 때 사용하는 계산식을 말합니다. 주로 아래와 같이 지수 형태로 표현하게 됩니다. 지금은 일단 이런 게 있다는 정도만 알면 됩니다.
x^8 + x^2 + x + 1
XOR
여러가지 논리 연산 중에 하나로, 다음의 4가지 경우를 가집니다.
- TRUE xor TRUE = FALSE
- TRUE xor FALSE = TRUE
- FALSE xor TRUE = TRUE
- FALSE xor FALSE = FALSE
xor 연산자의 왼쪽과 오른쪽에 들어가는 값이 같으면 FALSE를 반환하고, 두 개의 값이 다르면 TRUE를 반환합니다. 실제 CRC연산을 하는데는 이 논리 연산이 사용됩니다.
bitwise 연산
"bitwise" 라는 단어는 비트별로 연산한다는 뜻입니다. 만약에 1010 이라는 데이터와 0011 이라는 데이터를 bitwise and 연산을 한다고 하면, 각 비트 자릿수마다 and 연산을 수행하면 됩니다. 아래와 같습니다.

- bit.0 : 0 and 1 = 0
- bit.1 : 1 and 1 = 1
- bit.2 : 0 and 0 = 0
- bit.3 : 1 and 0 = 0
HEX
16진법을 뜻하며, 주로 "헥사"라고 읽습니다. 10진법이 0~9까지 값을 가지는 반면, 16진법은 0~9에 더해서 A~F까지 6개의 문자를 추가로 사용합니다.
CRC 계산 방법
예제로 설명하는 게 쉬울 거 같습니다. 주어진 조건이 다음과 같다고 하겠습니다.
- 데이터 : F1 AA 0B 39
- polynomial : x^8 + x^2 + x + 1
1단계 : 데이터를 비트로 변환
위의 예시 데이터는 HEX 값이구요, 이를 먼저 2진법인 비트로 변환해주어야 합니다. 위의 데이터를 비트로 변환하면 다음과 같습니다.
F1 AA 0B 39 = 1111 0001 1010 1010 0000 1011 0011 1001
2단계 : polynomial을 비트로 변환
위에서 잠깐 소개해드렸지만 polynomial 은 지수 형태의 식입니다. 변환은 간단합니다. 그러기 위해 먼저 위의 식을 조금 변형해 볼게요.
x^8 + x^2 + x + 1 = 1*x^8 + 0*x^7 + 0*x^6 + 0*x^5 + 0*x^4 + 0*x^3 + 1*x^2 + 1*x^1 + 1*x^0
x 앞에 1이 곱해져 있다고 상상하고, 중간중간 비어있는 승수는 0이 곱해졌기 때문에 그렇다고 생각하는 겁니다. 그리고 나서 앞에 붙어있는 계수만 싹 모아볼게요. 그러면 아래와 같습니다.
x^8 + x^2 + x + 1 = 100000111
이해가 되시나요? 위에 엄청나게 긴 식에서 앞에 계수만 따서 쓴 겁니다. 이제 데이터와 polynomial이 모두 준비되었으니 계산만 하면 됩니다.
3단계 : bitwise xor 계산하기
일단 재료들을 다시 한 번 써보겠습니다.
- 데이터 : 1111 0001 1010 1010 0000 1011 0011 1001
- polynomial : 100000111
데이터에 여분의 비트 붙이기
CRC는 일종의 나머지를 계산하는 개념이기 때문에, 원래의 데이터에 여분의 비트를 붙여줘야 합니다. polynomial 의 승수가 8이라면 8비트를 덧붙이고, 승수가 15라면 15비트를 덧붙입니다. 값은 모두 0으로 설정해 줍니다. 즉 이 데이터는 다음과 같이 변형됩니다.
- 원 데이터 : 1111 0001 1010 1010 0000 1011 0011 1001
- 변형된 데이터 : 1111 0001 1010 1010 0000 1011 0011 1001 0000 0000
끝에 0이 8개 더 붙었죠? 이 상태에서 진짜 계산을 시작해 줍니다.
데이터 맨 앞부터 xor 연산하기
이건 그림으로 설명하는 게 쉬울 듯 합니다. 예전에 사칙연산할 때 세로로 계산하던 거 기억나시나요? 그런 식으로 해줍니다.

변형된 데이터의 맨 앞부분에서 polynomial 을 xor 연산합니다. 그러면 맨 아랫줄과 같이 결과가 나오겠죠. 그 다음에 polynomial을 한 비트 오른쪽으로 옮겨주고, 같은 계산을 반복합니다.

보시면 한 비트가 옆으로 딱 이동했죠? 이런 식으로 계속 반복을 해주는 겁니다. 그러다가 보면 다음 단계에 도달할 겁니다.
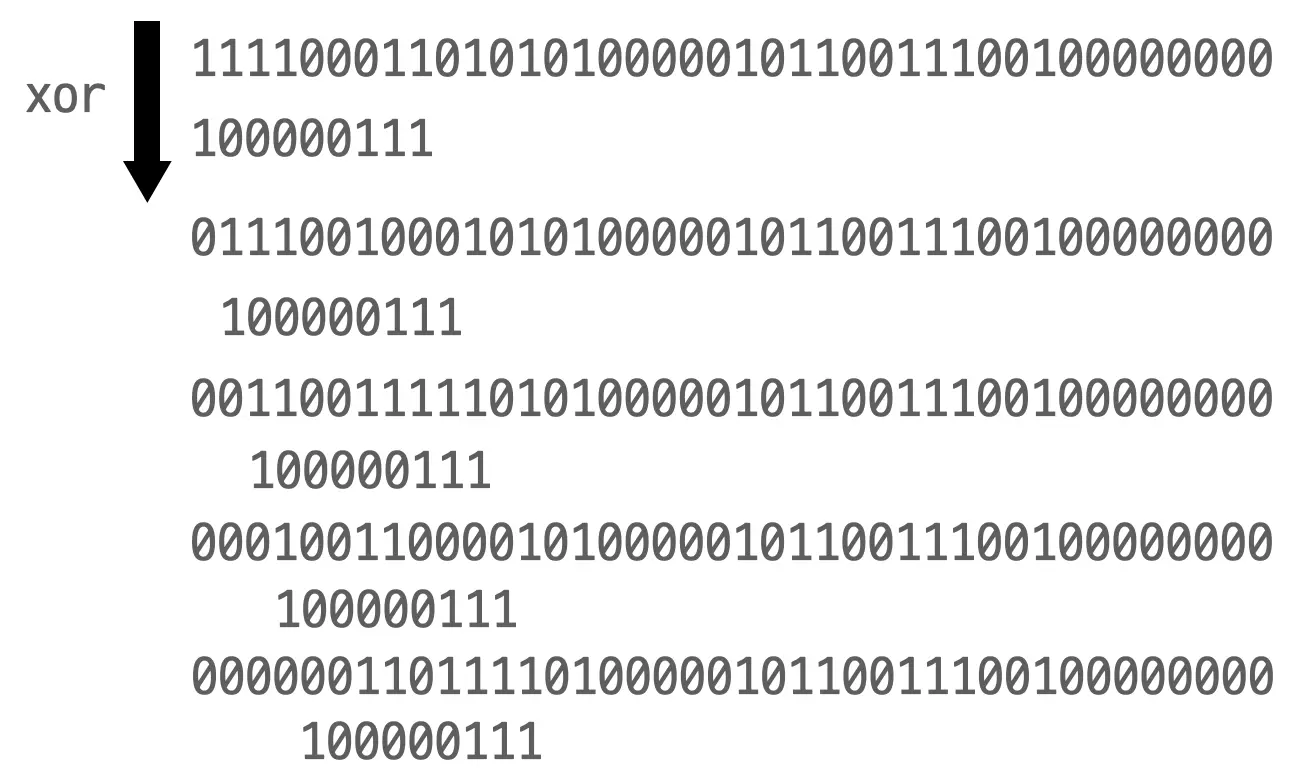
위 그림에서, polynomial 이 마지막에 도착한 위치를 보겠습니다. polynomial의 맨 앞자리 (x^8 위치)와 만나는 데이터 값이 0이죠? 이럴 때는 계산을 하지 않고 바로 다음 자리로 넘어갑니다. 1을 만날 때까지 넘어가면 되어요. 그래서 결국 아래와 같이 계산됩니다.

이쯤 되면 눈치채신 분도 계실 텐데, CRC 계산은 결국 원래의 데이터를 전부 0으로 만들어주면서 진행해 나가게 되고, 결국 맨 마지막에 덧붙여준만 뭔가 다른 값이 생기게 됩니다. 그게 일종의 나머지가 되고 그 값을 CRC 라고 부릅니다. 결국 위와 같이 계산해 나갔을 때의 최종적은 스텝은 아래와 같습니다.

원래 0으로 8개가 덧붙여 있던 부분이 다른 숫자로 채워졌습니다. 이게 이 데이터의 CRC가 됩니다.
데이터 송신하기
CRC 계산이 끝났으면 보통 원래의 데이터에 계산이 끝난 CRC를 붙여서 송신합니다. 이 예제의 경우에는 다음과 같아요.
- 원 데이터 : 1111 0001 1010 1010 0000 1011 0011 1001
- CRC : 1110 0010
- 송신하는 데이터 : 1111 0001 1010 1010 0000 1011 0011 1001 1110 0010
이렇게 송신하면 받는 측에서, 이 데이터를 그대로 위와 동일하게 CRC 계산 절차를 다시 수행합니다. 만약에 송신 상 오류가 없었다면 맨 마지막 8개 비트가 0000 0000 으로 됩니다. 이런 방식으로 데이터의 정합성을 체크하는 것이 CRC 이고, 계산 방식은 같은데 나머지가 나왔다가 0이 나왔다가를 반복한다고 해서 맨 앞에 "Cyclic"이라는 말이 붙었습니다.
댓글