클러스터링은 대체로 데이터 간의 거리를 정의하고, 거리가 가까운 데이터끼리는 하나의 클러스터로 묶는 방식으로 진행됩니다. 이때 다음을 정의해야 합니다.
- 거리(distance)의 정의
- 거리를 계산할 데이터의 정의
- 클러스터 갯수의 정의
이 중에서 대체로 클러스터링 방법에서 갈리는 것이 두번째와 세번째 항목인데요, 이 글에서 거리는 유클리드 거리로 정의하고, 나머지 두가지를 계층적 클러스터링에서 어떻게 다루는지 확인해 보겠습니다. 아예 예제로 살펴볼게요.
데이터를 정의하기
1단계는 데이터를 정의하는 겁니다. 이 샘플 클러스터링에는 단순하게 4개의 2차원 데이터로 정의해 볼게요. 다음과 같습니다.
| 데이터 | 좌표 |
| A | (1, 2) |
| B | (2, 1) |
| C | (3, 5) |
| D | (5, 6) |
위와 같이 정의된 데이터를 그림으로 보면 다음과 같습니다. 눈으로만 보면 딱 봐도 어떻게 클러스터링 되어야 하는지 알겠죠? 이제 바보같은 컴퓨터도 똑같이 할 수 있는지 보겠습니다.
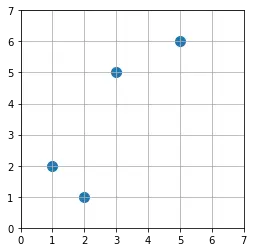
데이터 간의 거리를 계산하기
계층적 클러스터링의 경우 일단 모든 데이터가 하나하나의 그룹이라고 보고, 이 그룹끼리 조금씩 묶어나가는 방식으로 클러스터링을 진행합니다.
- 각각의 데이터를 각각의 그룹이라고 봄. 데이터가 4개면 그룹도 4개
- 모든 그룹 간의 거리를 계산
- 가장 가까운 그룹끼리 하나의 그룹으로 묶음 (예시. 데이터 2개를 묶어서 하나의 그룹이 되었다면, 4개 데이터에 3개 그룹)
- 2번, 3번 과정을 반복
위의 4개 과정을 지금의 예시로 확인해 보겠습니다.
초기 설정 : 각각의 데이터를 각각의 그룹이라고 봄.
위의 4개 데이터를 예시로 설정해 보겠습니다. 다음의 표를 보시죠.
| 그룹 | 데이터 | 좌표 |
| 1 | A | (1, 2) |
| 2 | B | (2, 1) |
| 3 | C | (3, 5) |
| 4 | D | (5, 6) |
위 표에서 각각의 데이터를 각각의 그룹으로 할당했습니다. 이제 다음 단계로 넘어가 볼게요.
1단계 : 모든 그룹 간의 거리를 계산
이제 모든 그룹끼리의 거리를 계산해 봅시다. 이때 자기 자신과의 거리는 계산에서 제외합니다. 일단은 다음의 표를 볼게요.
| 그룹 1 | 그룹 2 | 그룹 3 | 그룹 4 | |
| 그룹 1 | 제외 | 1.4 | 3.6 | 5.7 |
| 그룹 2 | 제외 | 4.1 | 5.8 | |
| 그룹 3 | 제외 | 2.2 | ||
| 그룹 4 | 제외 |
여기에서 표 아래쪽이 빈칸으로 되어 있는 것은, 이미 계산한 것과 동일한 값이기 때문입니다. 예를 들어 그룹 1과 그룹 2의 거리와 그룹 2와 그룹 1의 거리는 같기 때문에, 굳이 두번 적지 않은 겁니다.
2단계 : 가장 가까운 그룹끼리 하나의 그룹으로 합치기
위의 결과를 봤을 때, 그룹 1과 그룹 2의 거리가 가장 가깝습니다. 그러면 이 둘을 하나의 그룹으로 묶어야겠죠? 그 결과는 다음의 표와 같습니다.
| 그룹 | 데이터 | 좌표 |
| 1 | A, B | (1, 2), (2, 1) |
| 2 | C | (3, 5) |
| 3 | D | (5, 6) |
그룹의 번호는 뭉쳐질 때마다 계속 바뀌게 되니 무시하시구요, 데이터 A와 B가 하나의 그룹으로 통합되었다는 것에 주목하세요. 이 결과를 가지고 다시 거리 계산에 들어갑니다.
3단계 : 모든 그룹 간의 거리를 계산
1단계와 동일한 것 같지만 사실 완전히 똑같지는 않습니다. 왜냐하면 단일 데이터끼리의 거리는 그냥 유클리드 거리로 계산하면 되는데, 지금 위의 결과에서 그룹 1에는 데이터 2개가 들어있기 때문입니다. 그러니까 새로운 그룹 1과 그룹 2간의 거리는, 어떻게 계산해야 하는 거죠?
그룹 간의 거리의 정의
이때 그룹끼리 거리를 정의하는 데 뭔가 특별한 방법이 있는 것은 아니고, 그냥 상식적인 방법 하에 정하기 나름입니다.
- 그룹에 속한 데이터의 평균 위치를 그룹의 위치로 새로 정하고, 이 위치와 다른 데이터들 간의 거리를 구함
- 그룹에 속한 모든 데이터들과의 거리를 구한 뒤 이 중에 최소값을 거리로 정의
- 그룹에 속한 모든 데이터들과의 거리를 구한 뒤 이 중에 최대값을 거리로 정의
- 그룹에 속한 모든 데이터들과의 거리를 구한 뒤 거리를 평균함
제 생각에 3번째 방법 빼고는 모두 상식적이어 보이는데요, 그만큼 사실 결과에도 별다른 차이는 없습니다. 잘 되는 걸로 하시면 됩니다. 이해가 어려울 수 있으니, 아래의 도식화를 살펴볼게요.
그룹 간의 거리 정의 도식화
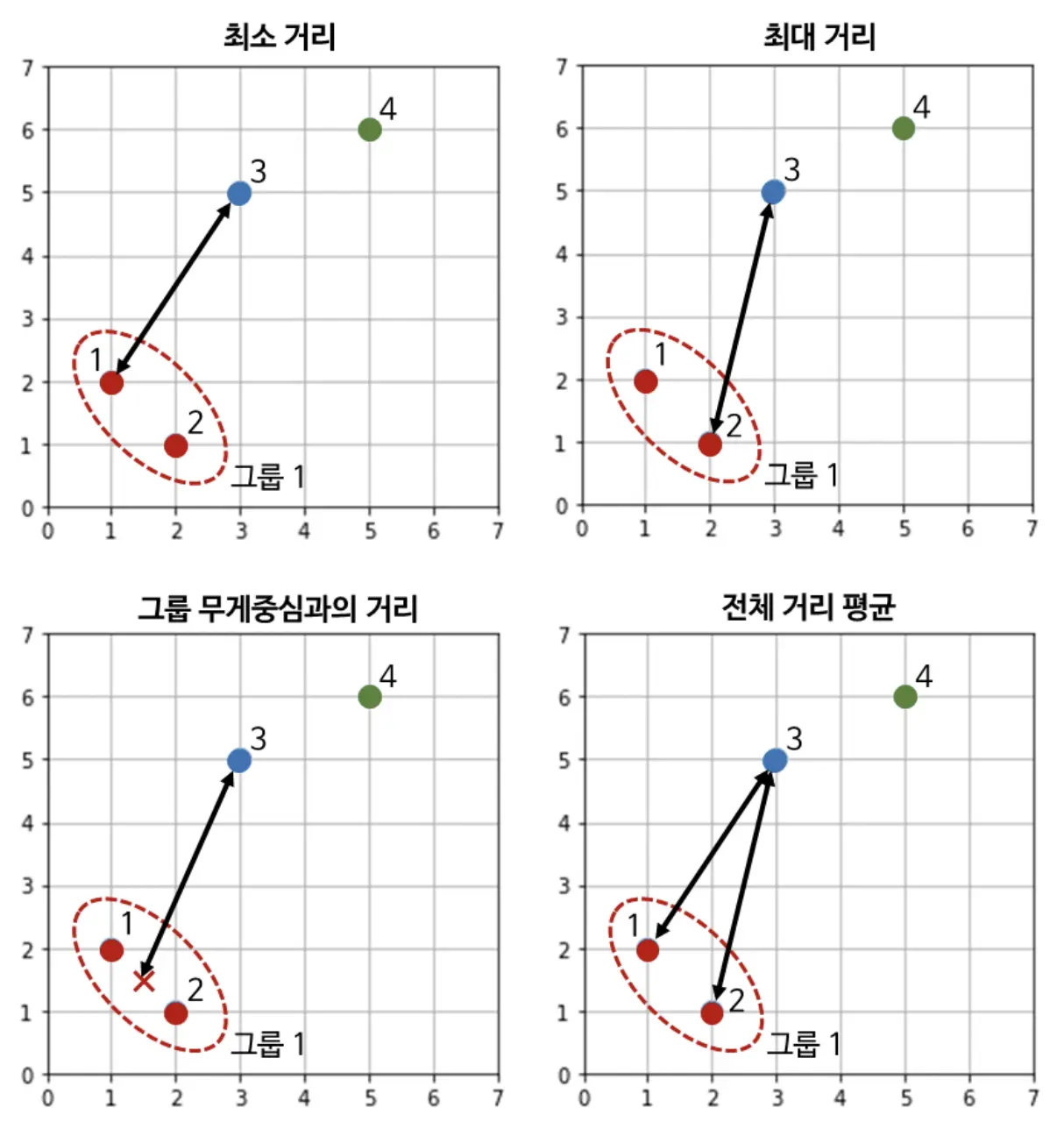
대충 최대값 말고는 다 말이 되어 보이는데, 참고로 scipy 패키지에서는 최소 거리를 사용합니다. 저는 이번 예제에서는 평균 거리를 사용해 보도록 할게요. 어차피 개념을 보고자 하는 것이니 뭘 해도 결과는 같습니다.
그룹 간의 거리 계산 결과
평균을 사용해서 거리를 계산한 결과는 다음과 같습니다.
| 그룹 1 | 그룹 2 | 그룹 3 | |
| 그룹 1 | 제외 | 3.9 | 5.7 |
| 그룹 2 | 제외 | 2.2 | |
| 그룹 3 | 제외 |
이번에는 그룹 2와 그룹 3이 합쳐지게 되었습니다.
4단계 : 2단계를 반복하기
앞의 결과를 이용해서 합친 결과는 다음과 같습니다.
| 그룹 | 데이터 | 좌표 |
| 1 | A, B | (1, 2), (2, 1) |
| 2 | C, D | (3, 5), (5, 6) |
이제 이걸로 한번 더 그룹 간의 결과를 계산해 볼게요.
| 그룹 1 | 그룹 2 | |
| 그룹 1 | 제외 | 4.8 |
| 그룹 2 | 제외 |
그룹 1과 그룹 2가 당연히 가장 가깝습니다. 그룹이 2개밖에 없으니까요. 이 단계에서는 모든 데이터가 하나로 합쳐지게 됩니다. 계층적 클러스터링은 이와 같이 끝까지 계산할 경우 모든 데이터를 하나로 묶어버립니다. 그러니까, 결국 사람이 보고 마지막 판단을 하게 되어 있어요.
계층적 클러스터링의 특징
클러스터링 방법은 사실 많습니다. 그 중에 계층적 클러스터링의 특징은 다음과 같은 것들이 있구요, 그로 인해 고민해 보면 좋을 포인트도 같이 알아볼게요.
K-means clustering과의 차이
K-means clustering도 이와 유사하게 클러스터의 갯수를 지정하게는 되어 있지만, 계층적 클러스터링이 그와 다른 점은 1 단위로 지정할 수는 없다는 점입니다. 그러니까 어느 정도 자연스러운 클러스터 갯수의 수준을 정하는 것이지 10개면 10개, 11개면 11개 라는 식으로 딱 사람이 정해놓고 갈 수는 없다는 거예요. K-means clustering은 그렇지 않죠. 아예 시작하기 전에 클러스터 갯수를 정하고 들어갑니다.
어떤 것이 좋은 것인가
분류의 목적에 따라 다르다고 할 수 있겠습니다. 사실 분류하고자 하는 갯수가 정확히 필요한 경우도 있지 않겠어요? 결국 이런 것들은 어떤 의사결정의 도구로써 사용될 때 의미가 있을 겁니다. 만약 10개로 반드시 분류가 필요한데 DBSCAN이나 계층적 클러스터링을 꼭 사용하겠다 라고 주장한다면 근본적인 면에서 맞지 않는 부분이 있을 것 같고, 목적에 맞는, 그리고 데이터의 특성에 맞는 분류 방법을 사용하는 게 중요할 것 같습니다.
부가 개념 : 덴드로그램
어디에서 끊는가라는 것을 시각화하는 것이라고 보면 됩니다. 데이터가 합쳐지는 순서를 눈으로 볼 수 있다는 장점이 있습니다. 위의 네 개 데이터를 가지고 수행한 결과를 덴드로그램으로 보면 다음과 같습니다.
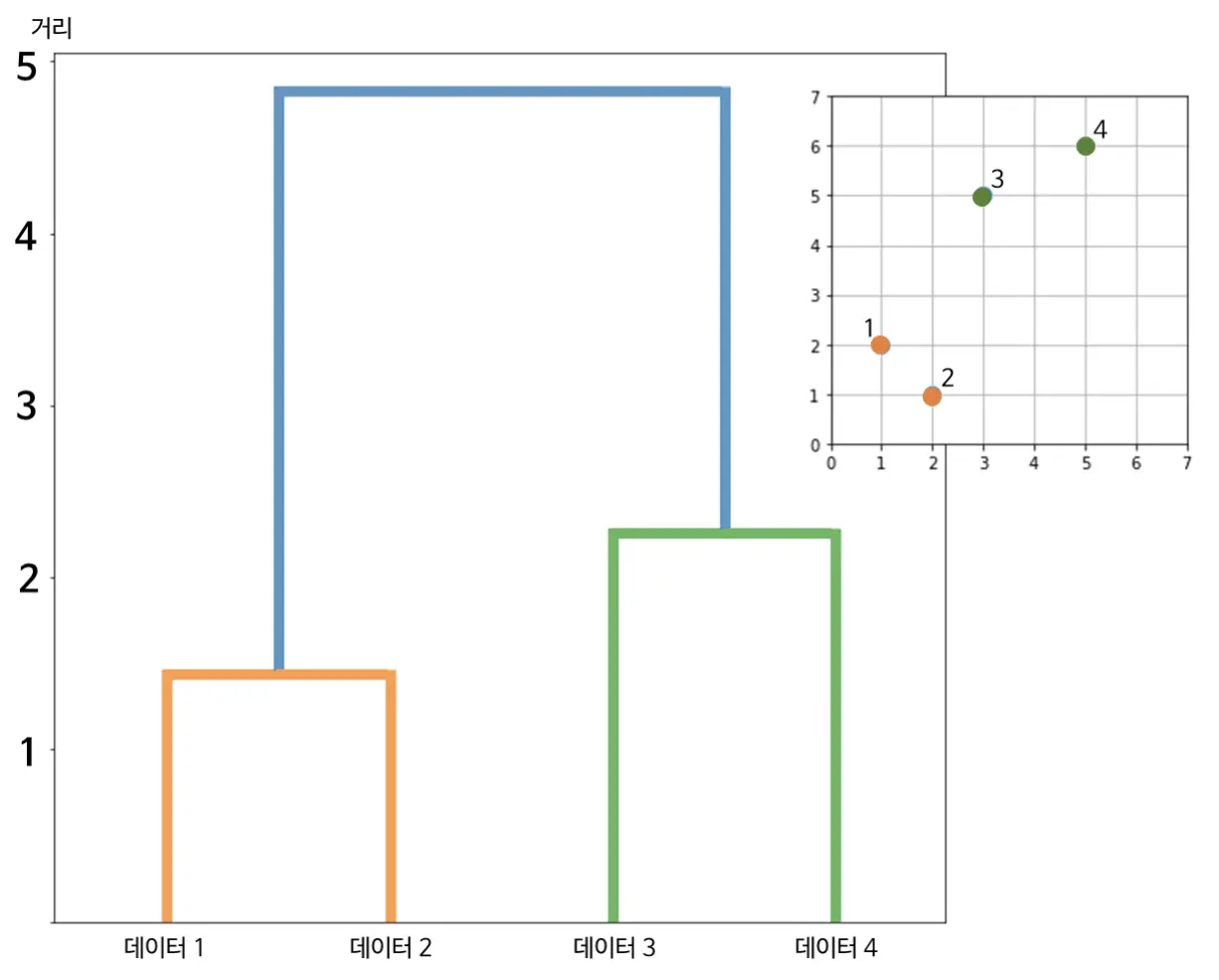
가로축은 데이터 번호, 세로축은 데이터 간 거리입니다. 계층적 클러스터링은 거리가 가까운 것부터 하나로 합쳤죠. 그래서 거리가 가까운 쪽에서 멀어지는 쪽으로 가다 보면 합쳐지는 순서를 볼 수 있습니다. 데이터 1과 2가 가장 먼저 하나로 합쳐지고, 그 다음 데이터 3과 4가 하나로 합쳐지고, 마지막으로 이 두개 그룹이 하나로 합쳐졌습니다.
제 생각에 이것의 쓰임새는 다음 정도인 거 같아요.
- 그럴싸함
- 눈으로 보면서 합쳐지는 수준을 적절히 정하고자 함
- 결과가 이상하다고 생각될 때 어떤 순서로 합쳐졌는지 알 수 있음
계층적 클러스터링을 이미지 검색해 보면 덴드로그램 이미지가 많이 나오는데, 그만큼 이 클러스터링의 성격을 잘 보여주는 그림이라고 할 수 있을 겁니다. 그런 면에서 그럴싸하다 라는 표현을 사용했어요. 어쨌든 뭐라도 하고 있는 거 같잖아요?
코드로 알아보기
코드는 아래와 같습니다. scipy 패키지를 이용한 코드입니다.
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage, cut_tree
# 데이터 만들기
num_data = 1
dimension = 2
data = np.random.randn(num_data, dimension)
offsets = np.array([[5,2], [-1,5], [2,3], [5,5], [-4,0], [4,-3],[6,8]])
for offset in offsets:
data = np.append(data,np.random.randn(num_data, dimension)*1.2 + offset, axis=0)
# 플랏
fig = plt.figure(figsize=[4,4])
plt.scatter(data.T[0],data.T[1], s=100)
plt.grid()
plt.show()
# 클러스터링하기
links = linkage(data, 'average')
# 덴드로그램 그리기
plt.figure(figsize=(12,12))
dendrogram(links, orientation='top', distance_sort='descending', show_leaf_counts=True)
plt.show()
# 클러스터 결과 시각화
num_cluster = 6
cluster = cut_tree(links, num_cluster).reshape(len(data)) # 데이터별 클러스터 반환
clustered = []
for i in range(num_cluster):
clustered.append(data[np.where(cluster==i)[0]])
fig = plt.figure(figsize=[10,10])
for clustered_data in clustered:
plt.scatter(clustered_data.T[0],clustered_data.T[1], s=6)
plt.grid()
plt.show()
이 코드로 샘플 데이터를 6개 그룹으로 나눠본 결과는 아래와 같습니다.
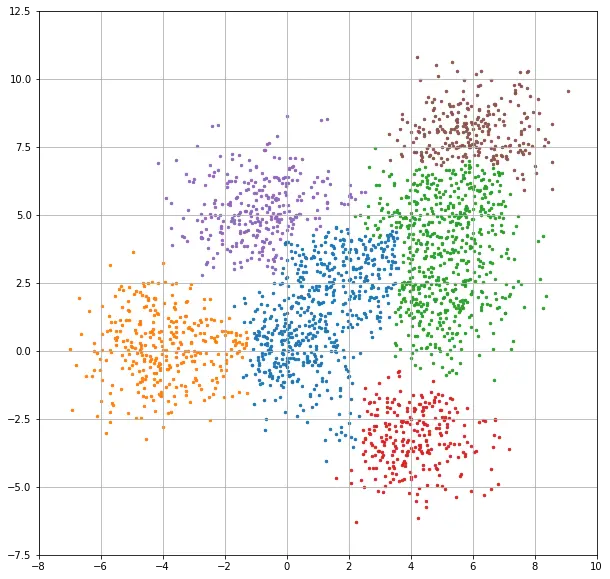
이거만 가지고는 잘 모를 수 있는데, K-means clustering 과 비교해 보면 좀 더 알기가 쉽습니다.
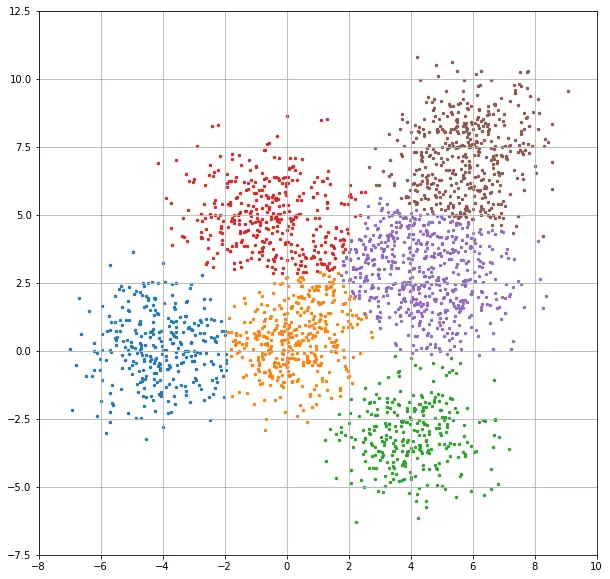
계층적 클러스터링이 조금 더 자연스럽게 나눠진 인상인데요, 이 결과는 클러스터 갯수를 3개로 했을 때 더 두드러집니다. 2개의 이미지를 연속으로 보여드릴게요.
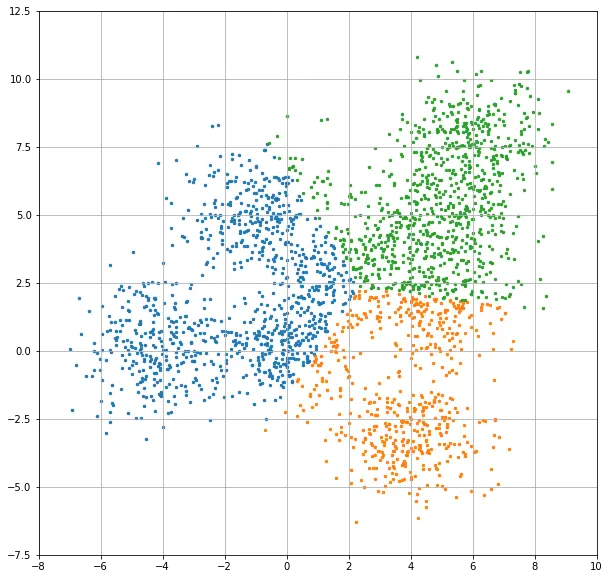
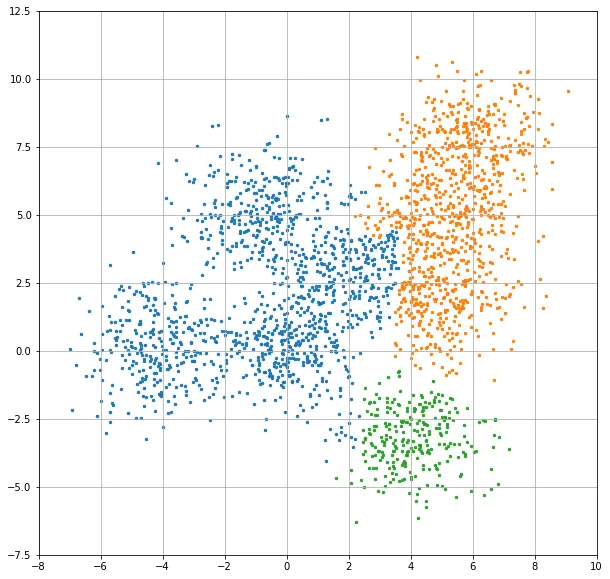
위쪽 이미지가 k-means clustering 이고 아래쪽은 hierarchical clustering 입니다. 계층적 클러스터링이 훨씬 자연스러워 보이죠? 하지만 이런 결과를 도출하기 위해 훨씬 더 많은 계산량을 요구합니다. 전체 데이터를 비교해야 하는 것이니까요. 데이터가 많아질수록, 데이터의 차원이 높아질수록 훨씬 느려질 수 밖에 없는 구조이기도 합니다.
댓글